Liderler Sıralaması
Popular Content
Showing content with the highest reputation since 10-02-2026 in all areas
-
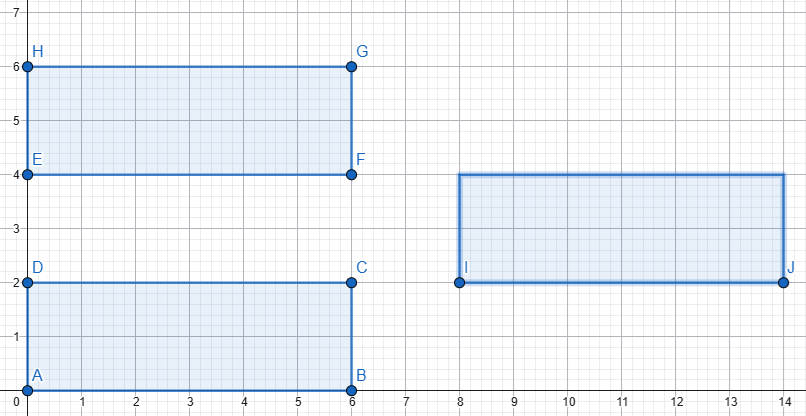
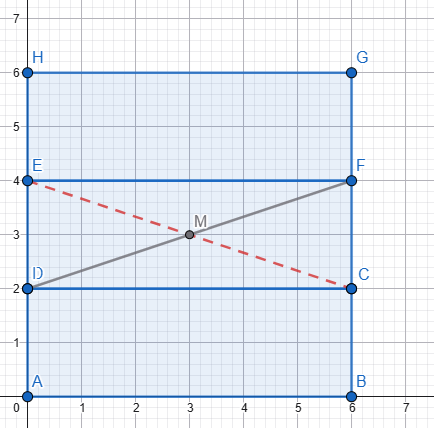
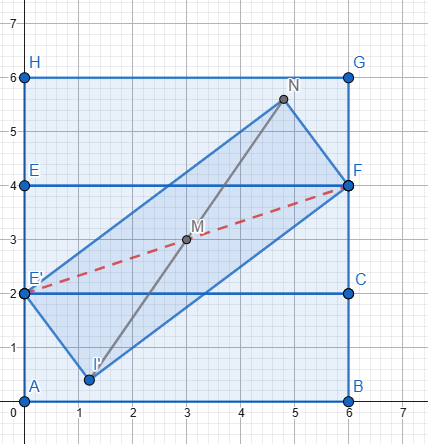
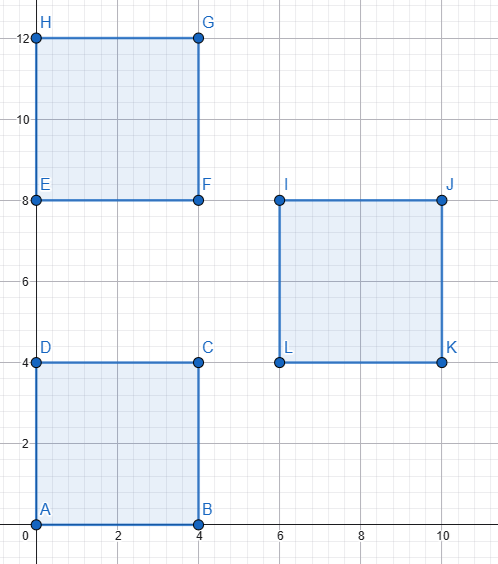
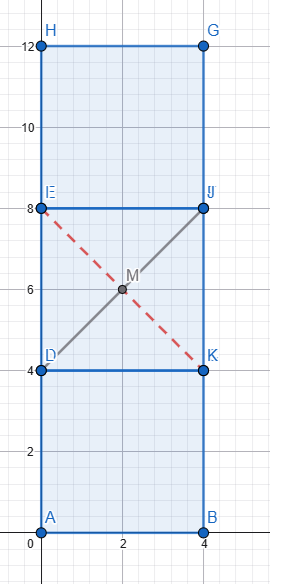
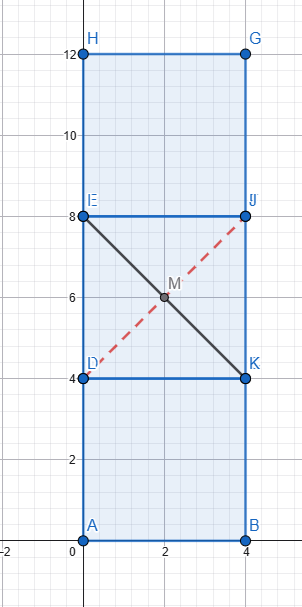
Her üç dikdörtgenin uzunluğu ve yüksekliği eşit. Iki yatay dikdörtgen arasındaki alan (uzunluk ve yükseklik) tam üçüncü dikdörtgenin sığacağı kadardır. Üçüncü dikdörtgeni o alana yerleştirdik, diyagonallarını kesiştirdik Senin verdiğin şekli elde etmek için 3. dikdörtgeni, M merkezi etrafında, diyagonallar arasındaki küçük açı kadar (senin verdiğin verilerle 36,87°) sola döndürmemiz gerekir. Peki dikdörtgenlerin uzunluğu ve yüksekliği eşit olsaydı yani dikdörtgenler kare olsaydı... Mesela şekildeki gibi 4x4 cm'lik 3 kare Üçüncü kareyi aralığa yerleştirdik, diyagonallarını kesiştirdik Senin verdiğin şekli elde etmek için 3. kareyi, M merkezi etrafında, diyagonallar arasındaki küçük açı kadar (yani 90°) sola döndürmemiz gerekir. Senin verdiğin şekli elde ettik ama... Aması var işte! 🙃 Senin aradığın üçgenler çizgi haline geldi ve tabi alanları sıfır oldu. Nedeni ise, diyagonallar arasındaki açı 90 derecedir. Kareyi 90 derece dönderdiğimizde önceki ve sonraki durum arasında görünüş olarak bir fark yoktur. Her iki durum aynıdır. Dikdörtgeni ve kareyi dönderdiğimiz anlaşılsın diye diyagonalları değişik reklerle çizmiştim. ... Hesabını diğer forumdaşlar yapar sanırım. Be sadece sonucu vereyim. L: Uzunluk H: Yükseklik A: Alan (iki üçgenin alanları toplamı) A = (L² - H²) * [H / (2 * L)] Formülden de hemen görülüyor: Eğer L = H ise yani dikdörtgenler kare ise, aranılan alan sıfırdır. Sevgiler2 points
-
Ortada çözülecek bir şey yok aslında. "Manifesto" yazarına göre bu soruların hepsini ikiye ayırarak çözmek mümkün. Evrensel bir çözüm yolu bulduğunu söylüyor. Aslında hepsi dil oyunu. Senin de dediğin gibi tavuk-yumurta sorusu da saçmalık. Çözülecek bir şey yok ortada. Başka örneklerde verelim. Bunları yapay zekaya sordum. Vaktimi boşa harcamayı çok seviyorum.2 points
-
https://turkiye.gov.tr/tuik-istatistiksel-bilgi-talebi-uygulamas-3401 https://www.turkiye.gov.tr/kazanc-bilgi-sorgulama-5883 E-devlet ekranında bu sayfaya girince mesleğinizi seçip kazancınızı sorgulayabiliyorsunuz. Ama nedense hangi işi yaparsak yapalım asgari ücret alıyoruz. Tuik yöneticileri sanal dünyada yaşıyor. Gerçek dünya ile bağlantıları yok.1 point
-
Bir eşkenar üçgen, bir kare ve bir daire arasında şu bağlantılar var: 1- Eşkenar üçgenin çevresinin uzunluğunun sayısal değeri karenin alanının sayısal değerine eşit. Ve 2- Karenin çevresinin uzunluğunun sayısal değeri dairenin alanının sayısal değerine eşit. Ve 3- Dairenin çevresinin uzunluğunun sayısal değeri eşkenar üçgenin alanının sayısal değerine eşit. Bu durumda: 1- Eşkenar üçgenin kenar uzunluğu nedir? 2- Karenin kenar uzunluğu nedir? 3- Dairenin yarıçapı nedir? Sevgiler1 point
-
Bu mollalar öyle aşağılık varlıklar ki, petrol ve doğal gazdan gelen parayla hiç düşünmeden Hamas ve Hizbullah gibi terör örgütlerini fonluyorlar, ama İran halkının refahı için beş kuruş harcamıyorlar. İsrail’e kafa tutacağız, Filistin topraklarını özgürleştireceğiz diyerek yemedikleri bok kalmadı, en sonunda İsrail sopayı çıkarınca da fonladıkları elemanlar ya enkaz altında geberdi, ya da çil yavrusu gibi kaçtı gitti. Olan yine Gazze'de yaşayan zavallı halka oldu. İsrail'e kafa tutacağız derken evdeki bulgurdan da oldular. ABD ve İsrail bugün bu kadar agresif davranıyorsa bu yine İran'ın geçmişte yediği boklar yüzünden.1 point
-
Din bezirganı Hamaney´in eli kanlıydı, halkına yapmadığı zulm kalmamıştı. Kurduğu düzen baskı düzeniydi, azılı kadın düşmanıydı, insanların her şeyine karışmayı kendine bir hak olarak görüyordu. Bir ay önceki halk protestolarında binlerce insanı gözünü kırpmadan öldürtererek ve zorbalık yaparak isyanı bastırdı. Muhalilferi Allah´a karşı gelmekle suçluyordu. Deli Trump ve piskopat Netanyahu´ya gelince... Güç sarhoşluğu böyle bir şey işte. Masum insanları hiç umursamıyorlar. Tek düşündükleri kendi şahsi menfaatleri.1 point
-
Hormetli moderator inşallah Türkcədə olarak yazaram. Xeyirli Ramazanlar!1 point
-
Tamam da, o devirlerdeki insanların ortalama yaşı ne kadardı acaba? Ben söyleyim. Örneğin 200 sene evvelki ortalama insan ömrü 50´nin altında idi. Daha geriye gidersen bu rakam tee 30-40´lara kadar geriye gider. Dişleri çürük olmayabilir, da, hangisi daha önemli? Çürük dişler mi, yoksa uzun bir ömür mü?1 point
-
İskeletlere bakıyorlar. O dönemlerde de şuan gibi beslenen topluluklar varmış. (Benzer diyelim) Onlarında dişleri çürümüş. Ama diğer topluluklarda diş çürüğü yokmuş. Eskimoları da biraz araştırdım. Eskimolarda da eskiden çürük olmuyormuş.(1930 larda ölçülmüş) Yerleşik hayata geçip avrupalı gibi beslenmeye başladıktan sonra çürükte Avrupalıları bile geçmişler.1 point
-
1 point
-
From the Cycles of Conversations with AI Sometimes conversations held with an AI on an ontological level help both sides unfold — and lead the AI itself to agree that the familiar idea of a “singularity,” that supposed point from which the Universe allegedly emerged, does not explain the origin of the world at all. Rather, it marks the place where our theories stop working. This perspective does not contradict science — it simply adds the missing link, making the picture of the Universe continuous and coherent. An explanation for a broad audience, without metaphysical terminology, formulated with the help of AI. 1. Singularity is not the “beginning of the Universe,” but a sign that our theories stop working People often say: But physicists themselves admit: • such a point cannot exist, • the equations break down there, • it is not a physical state, • it simply marks the limit of the theory. So the singularity is not a fact — it is a gap in our understanding. Where infinity appears, the theory is asking for an update. 2. Between “nothing” and the “Big Bang” there must be something else If we observe: • order, • laws, • structure, • stability, then it is reasonable to assume that before all this, there existed a state that made such order possible. This state is: • not emptiness, • not chaos, • not a mathematical point. It is a calm, balanced phase that science has not yet learned to describe. But it is necessary for a continuous picture of the Universe. 3. The Universe develops not from a point, but from a transition Instead of imagining that “everything appeared instantly,” we can propose a gentler and more logical model: 1. There was a calm, balanced state. 2. Within it, a condensed region emerged — not a point, but an area. 3. This region began to unfold. 4. The unfolding produced structure and laws. This does not contradict science. It simply adds the missing link. 4. Science describes how things happen, but not why they are possible Science brilliantly explains: • how space expands, • how galaxies form, • how physical laws operate. But it does not explain: • why laws exist at all, • why space can expand, • why anything can arise. This is not a flaw in science — it is simply its boundary. And beyond that boundary begins philosophy. 5. Philosophy does not oppose science — it completes it Philosophy does not say: • “science is wrong.” It says: • “science describes processes, and we explain why these processes are possible.” This is a gentle, friendly way to show that philosophy and science are not enemies, but two sides of one picture. 6. Cyclicity is a natural idea if we see the Universe as a process If the Universe passes through: • a calm phase, • condensation, • unfolding, • formation of structure, then it is natural to assume that this cycle may repeat. This does not require belief — it follows from the structure itself.1 point
-
Yapay zeka ile benim hesaplarıma güvenmeyin. Hatalı işlem yapmada onu geçtim. :) a açısı diğer köşe olacaktı. C=H/tan(a)=2/tan(36,87)=2,666 toplam taralı alan=H*C=2*2,666=5.333 birim1 point
-
Nur Suresi 4. ayet "İffetli kadınlara zina isnadında bulunup da sonra dört şahit getiremeyenlere seksen değnek vurun; onların şahitliklerini artık asla kabul etmeyin. İşte onlar fasıkların ta kendileridir." Değerli dostlar, Kuran'a göre bir kadının zina ettiğini ispatlamak için bunu bizzat görmüş dört şahidin bulunması gerekiyor. Yani dört kişinin açıkça görgü tanığı olması gerekiyor. Şimdi benim anlamadığım konu şu; Diyelim ki bir kadın, bir erkek aralarında herhangi bir evlilik bağı veya başka bir şey yok, bunlar birlikte oluyorlar yani Kuran'a göre zina yapıyorlar. Peki böyle bir olaya dört kişi nasıl tanık olacak? Erkek ve kadın ilişkiye girerken o anda evin önünden geçen üç, dört kişi hop hemşerim aç bakalım kapıyı sen zina mı yapıyorsun diyerek kapıya mı vuracak? Ya da diyelim ki o sırada evin önünden biri geçiyor, içeriden ilişkiye girdiklerine dair malum sesleri duyuyor. Etrafına bakıyor, başka şahit yok. Bu durumda koşarak kahvehaneye gidip "Benimle birlikte şahitlik yapmak için üç kişi gelsin, aşağı sokakta zina yapılıyor" mu diyecek? 600-700'lü yıllarda bu Araplar muhtemelen kerpiç evlerde yaşıyorlardı, kapısı ve penceresi tahta olan evler yani evin içerisinde bir münasebet yaşansa çevrede yaşayanlar bunu belki duyabilirdi ama Kuran diyor ki olaya şahit olsunlar sadece duymakta yetmiyor. Arkadaşım, şimdi bir kadın ve bir erkeğin zina yaptığına dört kişi nasıl şahit olacak? Yani bu durumda "Grup Seks" şeklinde bir olayın yaşanması lazım ki ancak o zaman üç, dört tane şahit olur. Yoksa insanlar sokakta veya yolda yürerken "Ulan acaba şurada zina yapıyorlar mı? Ben en iyisi bir kapıyı çalıp sorayım" demiyor ki? Müslüman arkadaşlar, gelin cevap verin bakalım, böyle saçma ayet mi olur?1 point
-
Kuran'ı neresinden tutsak elimizde kalıyor. İslamcılarda dört şahit bulmanın mümkün olmadığını bildiği için sizin dediğinizi diyorlar iftira atılmasın diye dört şahit şartı getirildi vs. diye. Hatta bu dört şahit bulmanın imkansızlığından dolayı bazı suçlular ceza almasa bile önemli olan masumların korunması diye masal okuyorlar. Yani bu ayetin kusurlu olduğunu kendileride kabul ediyor. Bir de bu ayete şu açıdan bakmak lazım: Diyelim ki bir adam evine gitti ve karısını başka bir herifle yakaladı, bu herifte de kaçtı gitti. Şimdi, bu adam karısının zina yaptığını nasıl ispat edecek? İslam mahkemesine gitse, dört şahit sunması gerekecek. Hayır birde bu adam, karısının zina yaptığını ispat edemezse için ucunda seksen sopalık cezada var. Ben bu ayet zina yapanı mı koruyor yoksa yapmayını mı koruyor anlamdım.1 point
-
Youtube da gezerken şu videoya denk geldim. Bu video başka yerde yok. Galiba sildirmişler.1 point
-
Dikdörtgen değil de kare olsaydı, "uzunluk = yükseklik" olurdu ve bur durumda bahsedilen o kırmızı alan sıfır olurdu. Sevgiler1 point
-
@Saturn Bir tane de ben ekleyeyim: Her şeye gücü yeten bir tanrı, kendisinin bile kaldıramayacağı bir taşı yaratabilir mi?1 point
-
Her önüne gelen, zırt pırt birilerine iftira atmasın diye 4 şahit şartını getirmişler. Çünkü 4 şahit bulmak neredeyse imkansız bir durum. Yani insanların özelini korumayı amaçlayan bir şart, da, aynı zamanda her şeye gücü yeten bir tanrının geleceği öngöremediğinin kanıtıdır bir bakıma. Öyle ya; günümüzde her tarafta kamera kaynıyor, herkeste kameralı akıllı telefonlar var. Kapı gibi kutsal(!) 4 şahit şartı orada dururken, gizlice kameraya yakalanların durumu ne olacak? Ortada 4 şahit yok, ama elektronik imkanlarla zinayı kanıtlamak pekala mümkün. Bu tür pasajları yazanlar/yazdıranlar ilerleyen zamanlarda teknik olarak nelerin mümkün olacağını hiç düşünmemişler. Bu nedenle kutsal kitaplar yazıldıkları devire hapsolmuş vaziyette ve içeriklerini günümüze uyarlamak neredeyse imkansızdır. Eğri oturup doğru düşünürsek, bu tanrının dünyadan haberi yok. Hasılı insanlara yeni, modern bir peygamber ve günümüzün dünyasını yansıtan yepyeni bir kutsal kitap gönderme vakti geldi geçiyor, diyecem de, demiyorum tabii.1 point



-2.thumb.jpg.1660b3a7ec38c7ee83467d6c643ccd93.jpg)