DreiMalAli

Ben İngilizce bilmem. Bilenler için Gazali'nin "Krallare Öğütler" kitabının İngilizcesinin linki: www.ghazali.org/books/kingcouncel.pdf Belki hayır sever birisi bana meselaaaa... Sayfa 164 ve 165'i özetler. Sevgiler

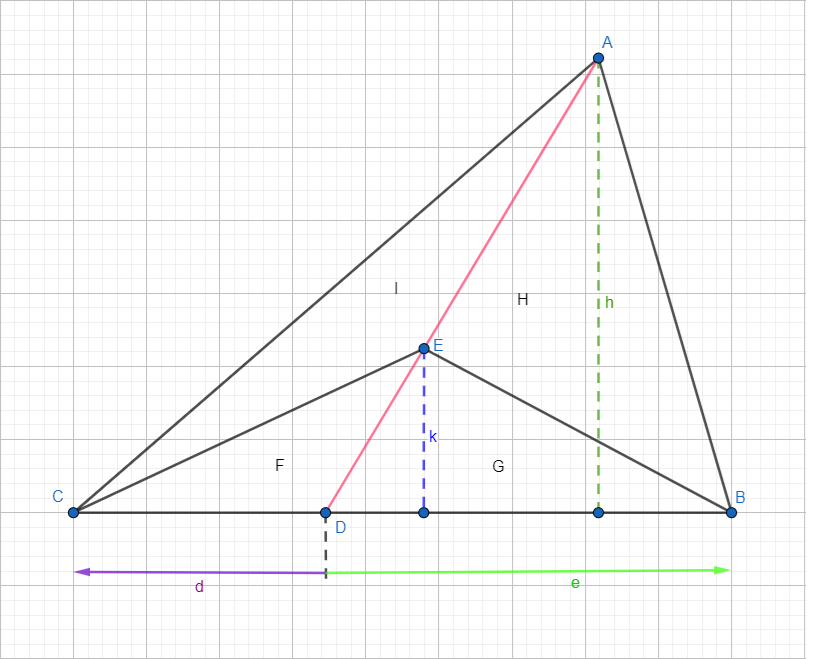
ABC üçgeni içinde herhangi bir E noktası alıyoruz. AE’nin uzantısı BC kenarını D noktasında kesiyor. ABC üçgeninin B ve C köşelerini E ile birleştiriyoruz. ABC üçgeninin yüksekliği h, EBC üçgeninin yüksekliği k olsun. DC = d BD = e F: CED üçgeninin alanı G: DEB üçgeninin alanı H: EAB üçgeninin alanı I: CAE üçgeninin alanı Üçgen alanları için şu eşitlikleri yazabiliriz: F = d*k/2 G = e*k/2 F + I = d*h/2 --> I = d*h/2 – F = d*h/2 - d*k/2 = d*(h – k)/2 G + H = e*h/2 --> H = e*h/2 - G = e*h/2 - e*k/2 = e*(h – k)/2 Komşu alanları oranlarsak F/I = k/(h – k) G/H = k/(h – k) Meğer komşu alanların oranları eşitmiş: F/I = G/H veya F/G = I/H Ayrıca F/G = (I + F)/(G + H) = d/e eşitliğine bir önceki eşitliğini de katarsak, F/G = I/H = (I + F)/(G + H) olur. Oranlama yönü göz önüne alındığında, hem komşu üçgenlerin oranları ve hem de komşu üçgenlerin toplamları oranları birbirine eşittirler. Sevgiler

Çay için gelmem ama kahve için hiç bir yol uzak değildir. 🫠 Sevgiler

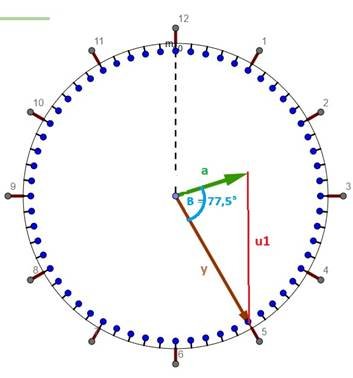
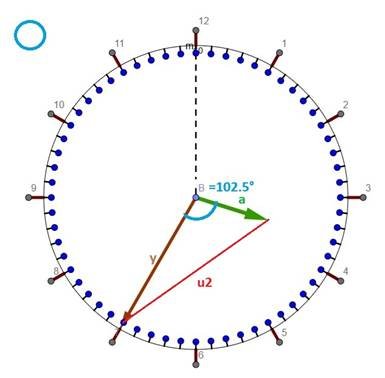
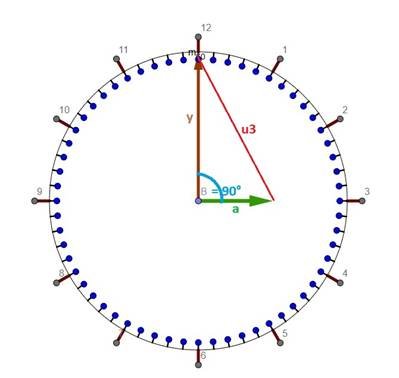
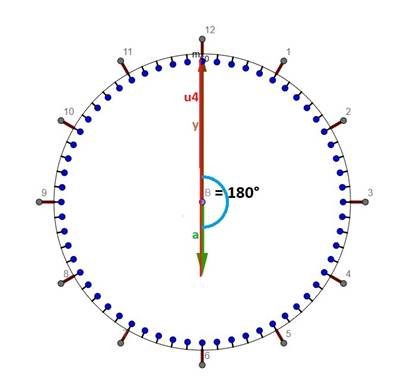
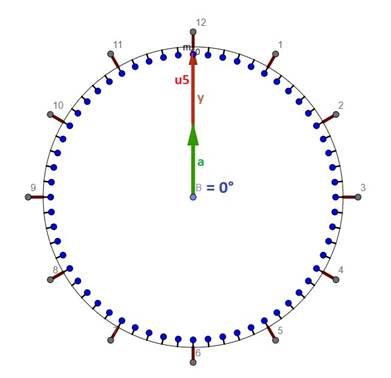
Saat 2:25’de analog saatın göstergelerinin konumu: Analog saatlarda göstergeler ve göstergelerin uçlarını birleştiren çizgi bir üçgen oluşturuyor. Soruda uçlar arası uzaklık, yani üçgenin bir kenarı (u1) veriliyor. Göstergeler arası açı ise verilen saat (2:25) ile belli olur. Bu iki veri ile üçgen hesaplamak mümkün olmadığı için ikinci bir saat (3:35) ve ikinci bir göstergeler arası uzaklık (u2) daha verilmiş. Saat 3:35’de analog saatın göstergelerinin konumu: Resimlerde - a = akrep (saat) göstergesinin uzunluğudur. - y = yelkovan (dakika) göstergesinin uzunluğudur. - B = akrep ve yelkovanın oluşturduğu açıdır - u1, u2 … verilen saatlarda akrep ve yelkovanın uçlarını birleştiren çizginin uzunluğudur. Göstergeler arası açı, göstergelerin açısal hızları yardımı ile hesaplanır. Wa ve Wy akrep ve yelkovanın açısal hızı, Ba ve By ise t zamanında kat ettikleri açılar olsun. Yelkovan 360 derecelik bir açıyı 1 saatta kat ettiği için açısal hızı Wy = By/t = 360°/1h = 360 °/h olur. Akrep ise 360 derecelik bir açıyı 12 saatta kat ettiği için açısal hızı Wa =Ba/t = 360°/12h = 30 °/h olur. Kat edilen açı zamana bağlı olduğu için her değeri alabilir. Ama saat ekranı üzerinde en çok 360 derece geçerli olduğundan, 360’ı aşan değerlerden 360’ları çıkarmamız gerekir. Matematiksel söylersek, açı hesaplarında modulo işlemi uygulamamız gerekir Yani Ba = Wa * t MOD 360 By = Wy * t MOD 360 olarak hesaplamamız gerekir. Saat 2:25’de durum: Saat 2:25 vaktinin saat birimi olarak zaman değeri: t = 2+25/60 h = 2+5/12 h = 29/12 h Akrepin aldığı açı Wa * t MOD 360 = 30*29/12 MOD 360 = 72,5° ‘dir. Yelkovanın aldığı açı ise By = Wy*t MOD 360 = 360*29/12 MOD 360 = 150° ‘dir. Göstergeler arası açı ise göstergelerin kat ettikleri açlar arasındaki farkın mutlak değeridir: B = |By – Ba| = |Wy*t - Wa*t| = |150 – 72,5| = 77,5° Buraya kadar gelmişken, sorudaki bütün zamanların açılarını da hesaplayayım. Saat 3:35’de durum: t = 3+35/60 h = 3+7/12 h = 43/12 h By = Wy*t MOD 360 = 360*43/12 MOD 360 = 210° Ba = Wa*t MOD 360 = 30*43/12 MOD 360 = 107,5° B = |By - Ba| = |210 – 107,5| = 102,5° Saat 3:00’da durum: t = 3+0/60 h = 3 h By = Wy*t MOD 360 = 360*3 MOD 360 = 0° Ba = Wa*t MOD 360 = 30*3 MOD 360 = 90° B = |By - Ba| = |0 - 90| = 90° Saat 6:00’da durum: t = 6+0/60 h = 6 h By = Wy*t MOD 360 = 360*6 MOD 360 = 0° Ba = Wa*t MOD 360 = 30*6 MOD 360 = 180° B = |By - Ba| = |0 - 180| = 180° Saat 12:00’de durum: t = 12+0/60 h = 12 h By = Wy*t MOD 360 = 360*12 MOD 360 = 0° Ba = Wa*t MOD 360 = 30*12 MOD 360 = 0° B = |By - Ba| = |0 - 0| = 0° Soruya geri dönersek… Saat 2:25 ve saat 3:35 verileri ile, bu saatlarda oluşan üçgenlere Kosinüs Teoremi uyguluyoruz. u1² = 161² = a² + y² - 2*a*y*cos(77,5°) u2² = 199² = a² + y² - 2*a*y*cos(102,5°) Bu, ikinci dereceden iki bilinmeyenli iki denklemden akrepin ve yelkovanın uzunlukları elbette hesaplanabilir. Daha kolayına ise: Q = a² + y² ve P = 2*a*y diye tanımlamaları ile erişilir. Göstergelerin (a ve y) uzunlukları değişmediği için, Q ve P de sabit kalır. P ve Q denklemlere yerleştirilirse u1² = Q - P*cos(77,5°) u2² = Q - P*cos(102,5°) birinci dereceden iki bilinmeyenli iki denklemimiz olur, işlemler basitleşir. Q ve P değerlerini saat kadrajında oluşacak her açı ve her üçgen için kullanabiliriz. İkinci eşitlikten birinciyi çıkarırsak, Q yok olur, P hesaplanır: P = (u2² - u1²) / [2* sin(12,5°)] = 31602,35… P değeri denklemlerin birisinde yerine konulursa, Q belirlenir: Q = u1² + P * cos(77,5°) = 32761. Veya: Q = u2² + P * cos(102,5°) = 32761. ------------------------------------------------------------------------------------------------------------------------- Saat 3:00 için göstergelerin konumu: Kosinüs Teoremi: u3² = a² + y² - 2 * a * y * cos(90) = Q - P * 0 = Q = 32761 u3 = 181 mm B açısı 90 derece olduğu için u3 uzaklığı elbette direk Pisagor teoreminden de hesaplanabilirdi. u3² = a² + y² = Q = 32761 u3 = 181 mm ------------------------------------------------------------------------------------------------------------------------- Saat 6:00 için göstergelerin konumu: Kosinüs Teoremi: u4² = a² + y² - 2 * a * y * cos(180) = Q – P * (-1) = 32761 + 31602,35 = 64363,35 u4 = 253,7 mm ------------------------------------------------------------------------------------------------------------------------- Saat 6:00 için göstergelerin konumu: Kosinüs Teoremi: u5² = a² + y² - 2 * a * y * cos(0) = Q – P * (1) = 32761 - 31602,35 = 1158,65 u4 = 34,04 mm ------------------------------------------------------------------------------------------------------------------------- Sorular için gerek yoktu ama göstergelerin uzunluklarını da bilmek istersek Q = a² + y² = 32761 P = 2*a*y = 31602,35 eşitliklerinden a ve y’yi hesaplamamız mümkündür. Kısaca… a = P/(2*a*y), Q = [P/(2*a*y)]² + y², 4*y^4 + 4*Q*y² + P² = 0. Bu, dördüncü derecen bir denklemdir. z = y² tanımı ile denklem ikinci dereceye dönüşür: 4*z² + 4*Q*z + P² = 0. Buradan 2 tane z bulunur. z’lerin karekökleri ise a ve y’dir: a = 109,83 mm. y = 147,87 mm. Umarım işlem hatası yapmamışımdır. Sevgiler

Orta Okul çağlarında Erich von Däniken'in kitaplarını heyecanla okurdum. Ne de olsa o zamanın en baba UFO'cusuydu. En tanınmış kitabına "Tanrıları Arabaları" ismini vermesi boşuna değildi tabi. Lise süresince gözümden iyice düştü. Çükü, en azından cümlelerinin lastik gibi olduğu, her eleştiriye sıvışacak açık kapı bıraktığı dikkatimi çekmişti. Sevgiler

Basiti ve gıcığı ile başlayalım. 🤡 B: Babanın şimdiki yaşı Ç: Çocuğun şimdiki yaşı B = Ç + 21 B + 6 = 5x(Ç + 6) Bu iki eşitliğe göre babanın şimdiki yaşı 81/4 sene = 20 sene 3 aydır, çocuğun şimdiki yaşı ise -3/4 senedir. Dikkat! Çocuğun yaşının işareti "eksidir"!!! Bu eksi sayıyı, çocuk henüz doğmamış diye yorumluyoruz. Ayrıca -3/4 sene -9 ay demektir. Peki hamilelik ortalama ne kadar sürüyordu? Tabi ki 9 ay. Demek ki çocuk 9 ay sonra Dünyaya gelecek! Yani bu, döllenme şimdi olmuş anlamına gelir ki, annenin bunu bilmesi mümkün değildir. Tabi an itibarı ile bunu baba da bilemez. Ve hatta... Bunu ben dahi bilemem! Bilirim dersem adım röntgenciye çıkar. 😁 Sevgiler

15 Sanırım 5 saniyenin altındaydı. Sevgiler

🤗 Tamam, şimdi oldu. Tüyo için teşekkürler. 6 x 6 = 24 5 x 5 = 19 6 x 5 = 0x1E 5 x 4 = 0x14 Sevgiler

🤩 Gora filminin "UFO gören masum köylü" sahnesindeki UFO'yu görünce kıskanmış, bu nedenle de yeni UFO modelleri geliştirmişlerdir. 🫠 Sevgiler

Demek ki uzaylılar teknoloji konusunda pek de ileri değillermiş. Baksana; metalleri bile hala elleri ile yontuyorlar. Uzaylı veya değil, birisi ne kadar usta da olsa elle yontarken ara sıra eli mutlaka kayar. 😁 Yontulan cisim düz değil de eğri büğrü ise; eyvah eyvah; hata üstüne hata yapar. 🤪 Sevgiler

Bu gün çözemedim. Ümidim yarına. Sevgiler

Yanlız değilsin. Sevgiler

Sevgili @kavak, iyi ki "arş" kelimesini Almanca kullanmıyorsun. Ama Taha 5'te kullanılabilir de. Madem tahta oturan Arap'ın Allah'ıdır, öyleyse Arap'ın Allah'ının bir kıçı vardır. Arap'ın Allah'ının kıçı varsa, Arap'ın Allah'ı fiziksel bir şeydir. Fiziksel olduğuna göre Evrenin içinde bir yerlerde olması gerekir. Madem Arap'ın Allah'ının kıçı var, öyleyse ara sıra tuvalete gitmesi de gerekir. Bu durumda kıç temizliği işin içine girer. Arap'ın Allah'ı kıçını siliyor mu, silmiyor mu? Silmiyorsa, topluluk içinde ayıpr oluyor mu olmuyor mu? Kıç temizliği yapıyorsa, acaba kıçını kendisi mi temizliyor yoksa kıç temizleyici hizmetçiler mi (melek, huri, iblis, cin vb.) var? Epey soru daha var ama şimdilik burada bırakayım. 🫣 Sevgiler

"Yaşamamış birisinin doğumu" ve/veya "Yaşamamış birisinin doğumu öncesi" cümleleri paradoks mu içeriyor? 🫣 😍 🤩 Sevgiler

Konu ile alakalı olduğu için Ateistforum'dan bir link vereyim. Yaşamamış Muhammed'in doğumundan önce yazılmış Kuran sayfaları 🤩 Sevgiler

Yukardaki iletimde verdiğim makale ve tabi resimler şu kitaptan alınmadır: https://schiler-muecke.de/index.php?title=Markus+Groß+%2F+Karl-Heinz+Ohlig+Schlaglichter&art_no=M0224 Makalenin ismi: "Ein früher Koranpalimsest aus Saana (Sanaa'dan Eski bir Kuran palimsesti*) (DAM01 - 27.1) Elisabeth Puin" Sayfa 461'den itibaren. .. Kitabın bazı kısımları -bahsettiğim bölümler ve resimler de dahil- internette, "books.google.de" adresinde herkese açıktır. Sevgiler *palimsest: Üzerindeki yazı yıkanarak silinmiş ve fakat zamanla tekrar görünür hale gelmiş parşömen.

Resimler Elisabeth Puin'in bir makalesinden alınmıştır. E. Puin makalesinde Saana Kuran Tomarları'ndan "Sanaa DAM 01-27.1, parşömen 2" sayfasını günümüz Kuranı ile karşılaştırıyor. Resimler, surelerin ve ayetlerin tercümesine gerek bırakmıyor. İki metin arasındaki büyük yazılım farkı hemen göze batıyor. -------------------------------------------------------------------------------------------------------------------------------------------- Resimlerin anahtarı: Son iki resim "Sanaa DAM 01-27.1, parşömen 2"nin orijinalinin resmidir. E. Puin'in başka bir makalesi "Sanaa DAM 01-27.1, parşömen 4 und 5" sayfalarını içeriyor. Bu gün, bahsettiğim bu ikinci makaledeki resimleri ayrıca buraya yüklemek zahmetine katlanmayacağım. Aramızda kalsın! Çoook ve yoğun istek üzerine bu zahmete katlanabilirim. 😉 🫠 Sevgiler

Sevgili gun. Zannettiğin yol doğrudur ve sanırım en basit çözüm yoludur. Çizdiğin resim de güzel olmuş. Hatta akrep ve yelkovanın yerlerini hassasiyetle konumlandırmışsın. 👍 Verdiğin açılar da doğru (77,5° ve 102,5°). Sadece Kosinüs Teoreminin yazılışında bir hata var: Formülde y^2 yerine y yazmışsın. İpucu: a akrepin uzunluğu, y yelkovanın uzunluğu, u1 = 161 mm: saat 2:25'deki akrep-yelkovan-uçları uzaklığı, u2 = 199 mm: saat 3:35'deki akrep-yelkovan-uçları uzaklığı, u3 saat 3:00'deki akrep-yelkovan-uçları uzaklığı, ... olsun. Verilen her iki zaman için Kosinüs Teoremini alt alta yazarsak, iki bilinmeyenli iki denklem elde ederiz. u1^2 = a^2 + y^2 - 2*a*y*cos(77,5°) u2^2 = a^2 + y^2 - 2*a*y*cos(102,5°) Bu iki eşitlikten a ve y elbette hesaplanabilir ama aslında a ve y'yi hesaplamaya gerek yok. Q = a^2 + y^2 ve P = 2*a*y tanımlaması ile Kosinüs Teoremini tekrar yazarsak, P ve Q kolayca hesaplanır. u1^2 = Q - P*cos(77,5°) u2^2 = Q - P*cos(102,5°) Saat 3:00 için de Kosinüs teoremini yazdığımızda eşitlikte yine P ve Q vardır, tek değişiklik saat 3:00'deki açı ve uçlar arası uzaklık olacaktır. u3^2 = Q - P*cos(AÇI3) Ve u3 hemen hesaplanır (Aramızda kalsın! 🫣 Bu saat için Kosinüs Teoremi Pisagor denklemine dönüşür) Sorunun diğer şıkları için de aynı yolu uygulayabiliriz. ... Not: a ve y'yi elbette P ve Q yardımı ile de hesaplayabiliriz. Sevgiler

Arabın Allahı ( = Kuranın yazarları) Kuranda kadınları muhatap almaz ve kadınlara direk hitap etmez. Ancak erkekler üzerinden emir, haber, laf gönderir. Psikolog olsaydım, bu tip bir erkeğin psikolojik sorunları hakkında bir şeyler yazardım. Sevgiler

İlgilenenler için: 12 Ağustosu 13 Ağustosa bağlayan gece en yoğun yıldız kayması (meteor) gözlenebilecek gecedir. İnterner taraması için "Perseid meteor yağmuru" tümcesini kullanabilirsiniz. Sevgiler

Bir analog saat... Saat 02:25'de akrep ve yalkovanın uçları arasındaki uzaklık 161 mm ve saat 03:35'de 199 mm ise, saat 3'te (03:00) uçlar arası uzaklık ne kadardır? Peki saat 6'da (06:00) ve 12'de (12:00) uçlar arası uzaklık ne kadardır? Sevgiler

Aynen öyle. Sahtekarın teki. İlk intihal (alıntı, plagiat) sahtekarlarından birisi: Çükü kitabının içi nerdeyse tamamen İbni Sina, dışı (kapağı) ise Gazzali. İnsan azmanı, insan ve özellikle de kadın düşmanıdır. Yazılarında zengin ve güçlülere yalakalığı hemen dikkat çekiyor. Bu nedenle asalak birisi olduğunu da söyleyebilirim. Sevgiler

Yanlış anlaşılmayı önlemek amacıyla belirtmiş olayım: - D noktası CB kenarı üzerinde herhangi bir noktadır. Herhangi bir açıortay veya kenarortay veya yükseklik vb. büyüklüklerle alakası yoktur. - E noktası ise AD doğrusu üzerinde herhangi bir noktadır. Başka bir özelliği yoktur. Sevgiler

İpucu ve/veya önbilgi amacıyla önce şu soruyu çözmeyi dene. I = ACE üçgeninin alanı F = CDE üçgeninin alanı G = DBE üçgeninin alanı H = BAE üçgeninin alanı. k ve h CB kenarına diktir. Her ikisi de içinde bulundukları üçgenlerin yüksekliğidir. Alan hesabı için gerekecekler. Bu verilerden I, F, G ve H alanları arasında ve sadece I, F, G ve H içeren bir bağlantı bulursun. Daha doğrusu alanların oranları arasında bir bağlantı bulusun. Bu bağlantıyı yukardaki asıl soruda da kullanırsan, dörtgenin aranan F4 alanını bulursun. Sevgiler

Ayrıca internette okudukları her zırvayı irdelemeden, düşünmeden, soruşturmadan gerçekmiş gibi algılıyorlar. O da yetmezmiş gibi, forumlara, çevresine vb. kakalamaya çalışıyorlar. Sevgiler