-
İçerik sayısı
223 -
Kayıt tarihi
-
Son ziyareti
-
Kazandığı günler
35
DreiMalAli last won the day on 18 Şubat
DreiMalAli had the most liked content!
Sitemizdeki itibarı
66 ExcellentProfile Information
-
Gender
Not Telling
Son profil ziyaretçileri
2.487 profil görütülenme
-
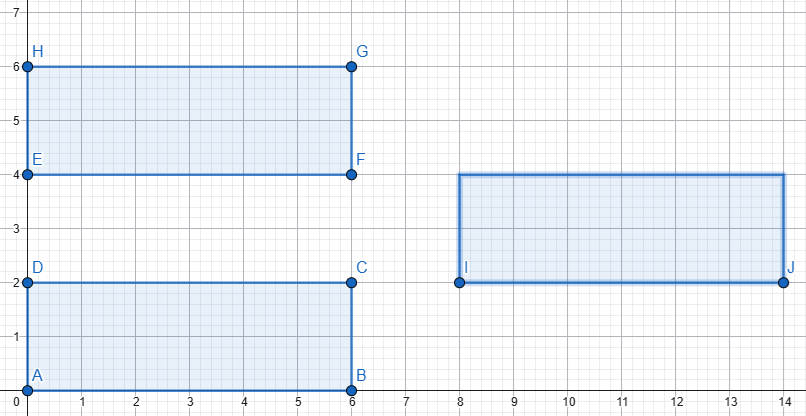
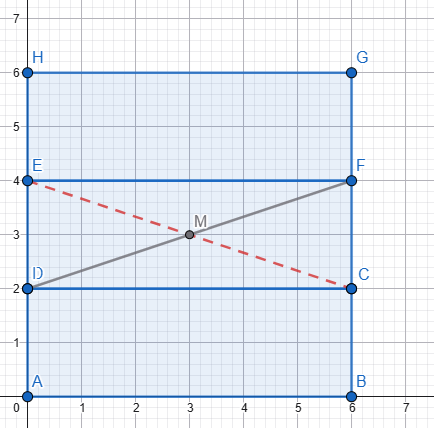
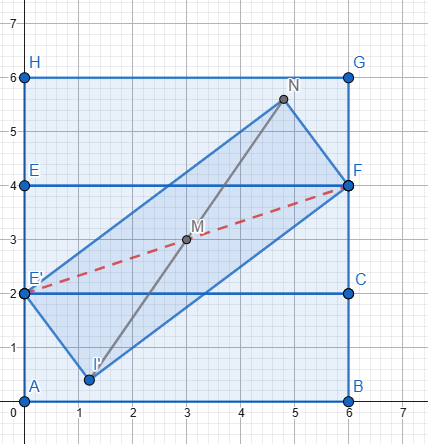
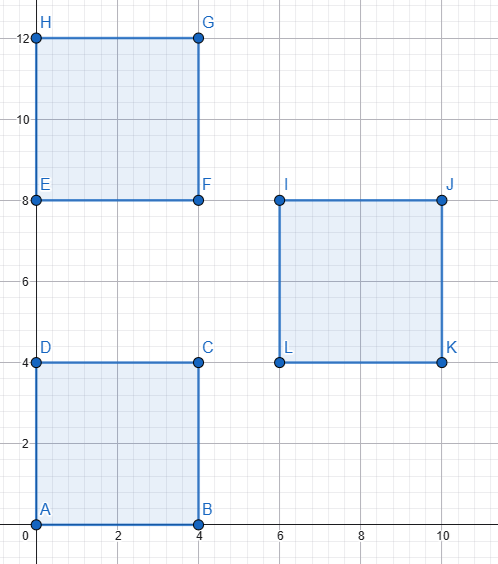
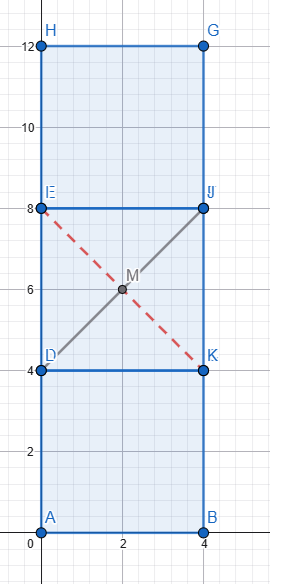
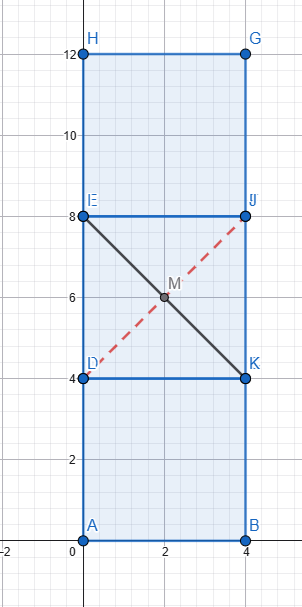
Her üç dikdörtgenin uzunluğu ve yüksekliği eşit. Iki yatay dikdörtgen arasındaki alan (uzunluk ve yükseklik) tam üçüncü dikdörtgenin sığacağı kadardır. Üçüncü dikdörtgeni o alana yerleştirdik, diyagonallarını kesiştirdik Senin verdiğin şekli elde etmek için 3. dikdörtgeni, M merkezi etrafında, diyagonallar arasındaki küçük açı kadar (senin verdiğin verilerle 36,87°) sola döndürmemiz gerekir. Peki dikdörtgenlerin uzunluğu ve yüksekliği eşit olsaydı yani dikdörtgenler kare olsaydı... Mesela şekildeki gibi 4x4 cm'lik 3 kare Üçüncü kareyi aralığa yerleştirdik, diyagonallarını kesiştirdik Senin verdiğin şekli elde etmek için 3. kareyi, M merkezi etrafında, diyagonallar arasındaki küçük açı kadar (yani 90°) sola döndürmemiz gerekir. Senin verdiğin şekli elde ettik ama... Aması var işte! 🙃 Senin aradığın üçgenler çizgi haline geldi ve tabi alanları sıfır oldu. Nedeni ise, diyagonallar arasındaki açı 90 derecedir. Kareyi 90 derece dönderdiğimizde önceki ve sonraki durum arasında görünüş olarak bir fark yoktur. Her iki durum aynıdır. Dikdörtgeni ve kareyi dönderdiğimiz anlaşılsın diye diyagonalları değişik reklerle çizmiştim. ... Hesabını diğer forumdaşlar yapar sanırım. Be sadece sonucu vereyim. L: Uzunluk H: Yükseklik A: Alan (iki üçgenin alanları toplamı) A = (L² - H²) * [H / (2 * L)] Formülden de hemen görülüyor: Eğer L = H ise yani dikdörtgenler kare ise, aranılan alan sıfırdır. Sevgiler
-
Dikdörtgen değil de kare olsaydı, "uzunluk = yükseklik" olurdu ve bur durumda bahsedilen o kırmızı alan sıfır olurdu. Sevgiler
-
Verdiğin resimde belirtilen yerler korunmuş alanlar değildirler. Onlar, rüzgar türbinleri için uygun olmayan alanlardır. Sevgiler
-
Cihan Karaosmanoğlu'nun "Hz. Akıl ve Dinler" isimli kitabı... Sevgiler
-
Sevgili @Saturn. Niye özellikle benim ismim geçti anlamadım. Bence soru bütün forum katılımcılarına olsun. Ve haklısın: Soruyu çözmek kolay. Ahmet'in bu günkü yaşı 31'dir. Berk'in bu günkü yaşı 19'dur. Can'ın bu günkü yaşı 22'dir. 12 sen önce Ahmet Berk'in şimdiki yaşındaydı ve Can 10 yaşındaydı. 12 sene sonra Berk Ahmet'in şimdiki yaşında olacak ve Can 34 yaşında olacak. Eğer sen gerçekten yapamadıysan, bir ip ucu vereyim: Yaş sorularında her zaman geçerli olan bir kural vardır. Bu kural, "iki şahsın yaş farkı her zaman sabittir" kuralıdır. Birinin yaşı A_şimdi (A_eski, A_gelecek) diğerinin yaşı B_şimdi (B_eski, B_gelecek) ise A_şimdi - B_ şimdi = A_eski - B_eski = A_gelecek - B_gelecek = S_AB = sabit. Çözüm için daha fazla yardım gerekirse, haberim olsun. Sevgiler
-
İyi de... Ben nerede hata yapıyorum ki? Sen de 5'er 5'er satıyordun ben de 5'er 5'er satıyordu. Nihayetinde ikisini topladım 10'ar 10'ar sattım. Sen 2 elmayı 5 Avroya satıyordun, ben 3 elmayı 5 avroya satıyordum. Nihayetinde ikisini topladım 5+5=10 elmayı 2+3=5 Avroya sattım. Burda bir mantık hatası görüyor musun sen? Veya diğer forum sakinleri? Sevgiler
-
Sorduğun bu soru, bildiğim, epeyce eski ve çözümü basit bir bilmecedir yahu. "tüm etiketleri yanlış iliştirilmiş" tümcesini ciddiye alırsın ve "Elma-Armut-Karışık" sandığından bir meyve çekersin. Gerisi çorap söküğü gibi gelir. 1- Elma çektiysen, o kasa elma kasasıdır. Armut etiketli kasa ise "Elma-Armut-Karışık" sandığıdır. Elma etiketli sandık ise elbette armut sandığıdır. 2- Armut çektiysen... 🫣 🫣 🫣 .. Anlaşıldı! Elma sattığımız günlerden kalma öfken hala geçmemiş, hatamı söylemeye de niyetin yok. 😁 Belki diğer forum sakinleri elma satışımızdaki suçumu/günahımı/hatamı açıklarlar... Da... Ben de nihayet rahatlarım. 🫠 Sevgiler
-
@kavak Yok yahu, hesap kitaptan anlamayan benim. Bana neden bozulduğunu hala bilmiyorum. Her karşılaşmamızda, sanki belediye otobüsünde ayağına basan benmişim gibi, ne o bakışlar? 😟 Sevgiler
-
Yıllar önceydi, ben ve @kavak pazarda elma satarak hayatımızı kazanıyorduk. Hem ben hem de kavak 60 elma ile çıkardık pazara. kavak 2 elmayı 5 Avroya satardı. Ben ise 3 elmayı 5 Avroya satardım ve her gün 100 Avro kazanırdım. Bir gün kavak, o gün pazara gelemeyeceğini, çünkü hasta olduğunu söyledi. Onun elmalarını da satmamı rica etti. Ne demek, elbette... Razı oldum tabi. Ama fiyat konusunda kafam karıştı: Aynı masada, aynı elmalar; ama iki elma kümesi ve iki değişik fiyat! Kümenin birisinde 2 elma 5 Avro diye yazıyor, diğerinde 3 elma 5 Avro diye... Olmazdı tabi! Bunun yerine benim 3 elma 5 Avro ile kavak'ın 2 elma 5 Avrosunu topladım, 5 (2+3=5) elmayı 10 (5+5=10) avroya satmaya karar verdim ve elmaların hepsini bu fiyatla sattım, bitirdim. Akşam kavak'a uğradım, toplam paradan benim 100 Avromu cebime attım, gerisini kavak'a verdim. Vermez olaydım! kavak parayı sayınca "DreiMalAli boyundan utan, benim paramı çalmaya utanmıyor musun? Ayıp diye bir şey var yahu! ..." benzeri bir ton laf saydı. O gün, bu gündür aramız hiç iyi değil, bana hala kızgın. Bana neden kızdığını, neden küstüğünü hala anlamadım. Sevgiler
-
😇 Harcamaları daha düşük miktarlarla yapsaydın, çok zengin olmuştun. Mesela her seferinde 1 liralık harcasaydın, şimdi 125 250 liran olurdu. Sevgiler
-
Maalesef desmos'u ben de bilmiyorum, henüz kullanmadım. Sadece bir kaç sefer @gun'ün desmos'taki formüllerine maydanoz olmuştum. Başkaca bir tecrübem olmadı. @gun desmos'ta güzel şeyler yapıyordu, dişli simulasyonu, parvane benzeri hareketli şeyler... Sevgiler
-
@gun cevabı gördükten sonra yine desmos ile güzel bir şeyler yapar ve buraya postalar diye tahmin etmiştim. Bu sefer tahminimde yanıldım galiba. Sevgiler
-
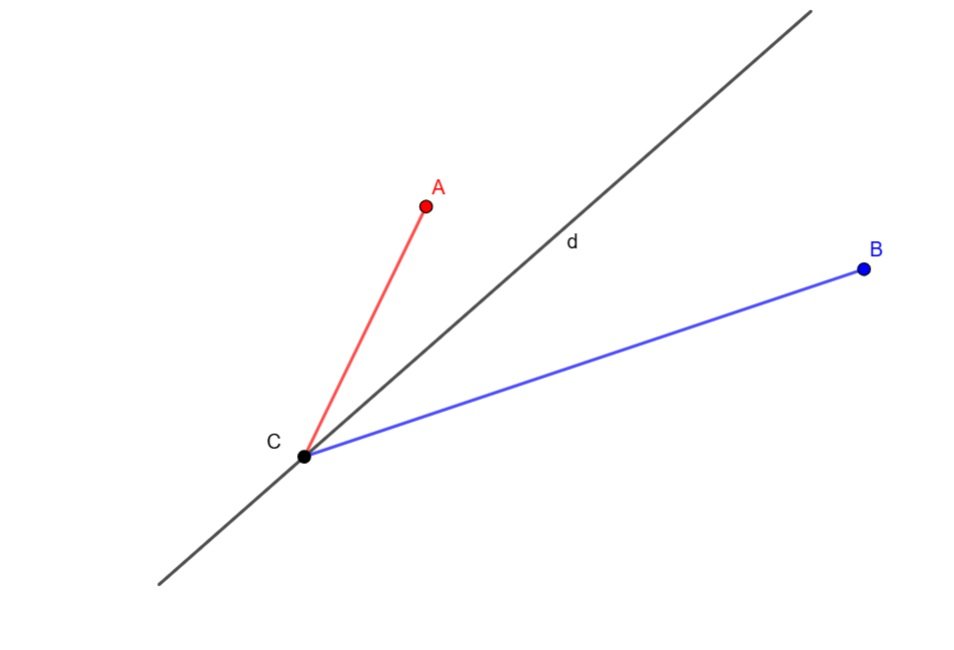
d doğrusunun bir tarafında A noktası, diğer tarafında ise B noktası bulunuyor. d doğrusu üzerinde nerede bir C noktası aldığımızda BC uzaklığı ile AC uzaklığı farkı en büyük olur? |BC - AC| = maximum! Sevgiler
-
Cevap: A 1- Üstte, solda birinci dokuzlu karenin birinci satırındaki kırmızı kare sola çekilince, sağda alt sırada, ikinci bir kare daha içeri çekiliyor. Böylece birinci sıranın ortadaki ikinci dokuzlusunun deseni oluşuyor. Üst sırada ortadaki ikinci dokuzlunun kırmızı kareleri sola çekilince, sağda alt sırada üçüncü bir kare daha içeri çekiliyor. Böylece birinci sıranın üçüncü dokuzlusu oluşuyor. 2- Ortada, solda birinci dokuzlu karenin birinci sütunundaki kırmızı kare aşağı çekilince, üstte ortadaki sütunda, ikinci bir kare daha içeri çekiliyor. Böylece ikinci sıranın ortadaki ikinci dokuzlusunun deseni oluşuyor. Orta sırada ortadaki ikinci dokuzlunun kırmızı kareleri aşağı çekilince, üstte sağdaki sütunda, üçüncüi bir kare daha içeri çekiliyor. Böylece ikinci sıranın üçüncü dokuzlusunun deseni oluşuyor. 3- Altta, solda birinci dokuzlu karenin kırmızı kareleri yukarı çekilince, altta sağdaki sütunda, üçüncü bir kare daha içeri çekiliyor. Böylece üçüncü sıranın ortadaki ikinci dokuzlusunun deseni oluşuyor. Alt sırada ortadaki ikinci dokuzlunun kırmızı kareleri yukarı çekilince, soldan birinci sütundaki kare kaybolur, Orta ve sağ sütunlardaki kırmızı kareler A şıkkının desenini oluştururlar, ki bu aynı zamanda soru işareti yerine konulması gereken dokuzludur. Yani cevap A'dır. Sevgiler
-
Cevaplardan birisi A şıkkıdır. Aramızda kalsın: Kendimce bir cevap bulmam 10 saniyeden fazla sürdü sevgiler